State-of-the-Art Exact Binary Vector Search for RAG in 100 lines of Julia
May 16, 2024
Updates
Thanks for HN users
mik1998andborodiwho brought up the popcnt instruction and the count_ones function in Julia which carries this out, I've updated the timings and it's even faster now.
Whether you use Int8, UInt8, or Int64 the performance the same when performing the actual search (on my M1 air). This might change depending on the architecture you're using. The best representation is probably UInt64s. as this will likely give you the most transferrable result across different architectures.
The best search timings come from either 1) Vector of StaticArrays and StaticArray query vector or 2) Matrix of elements as (num_bytes, num_rows) and StaticArray query. So could only make the query array static and get the same performance.
This is an experiment in how quickly precise RAG lookups could be performed with a binary vector space.
What is RAG?
"Retrieval Augmented Generation" (RAG) is augmentation to LLM content generation. The basic architecture is to call the LLM API with a prompt and query.
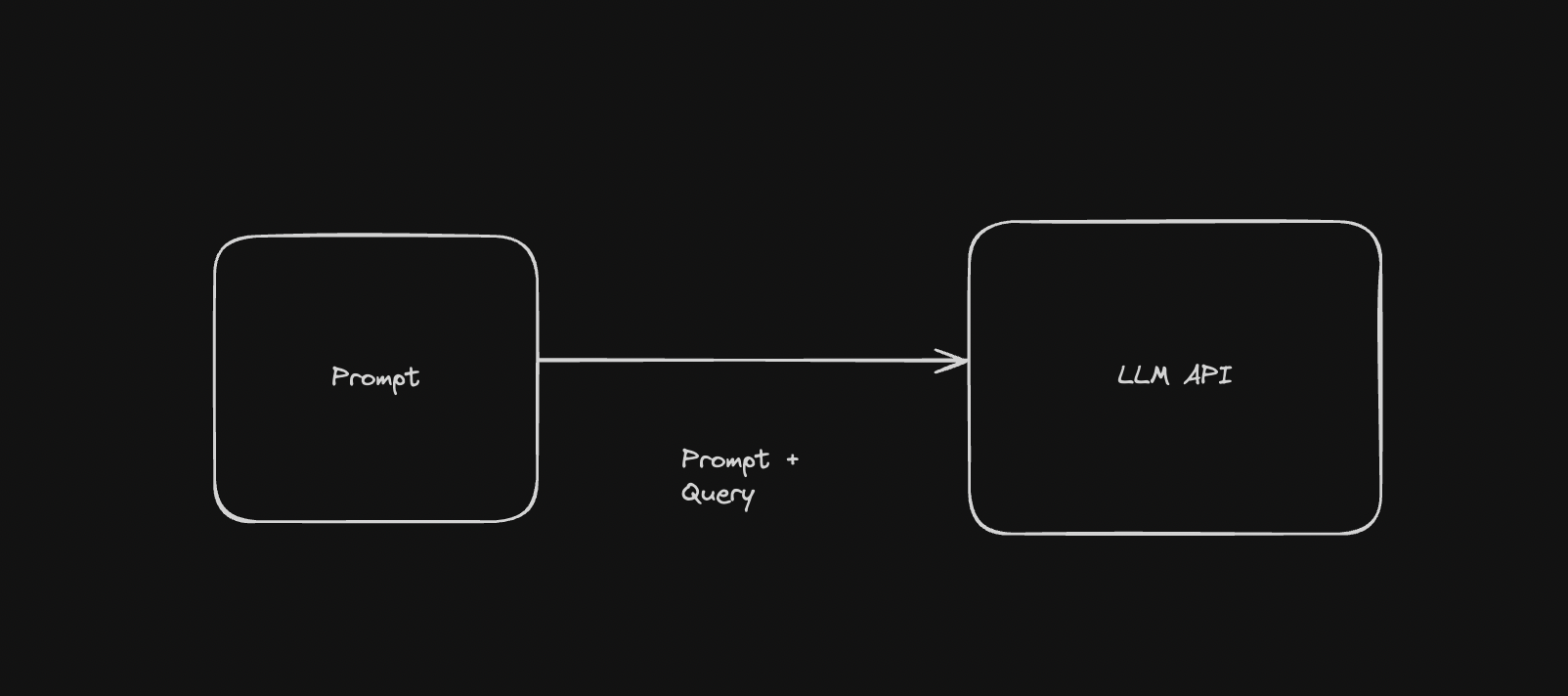
But sometimes we would like to programmatically add context to the prompt so that the query can be better answered. This is especially useful if we want to query internal documents, which the LLM should have no knowledge of, or simply improve the Q/A capabilities of the LLM in a specific domain.
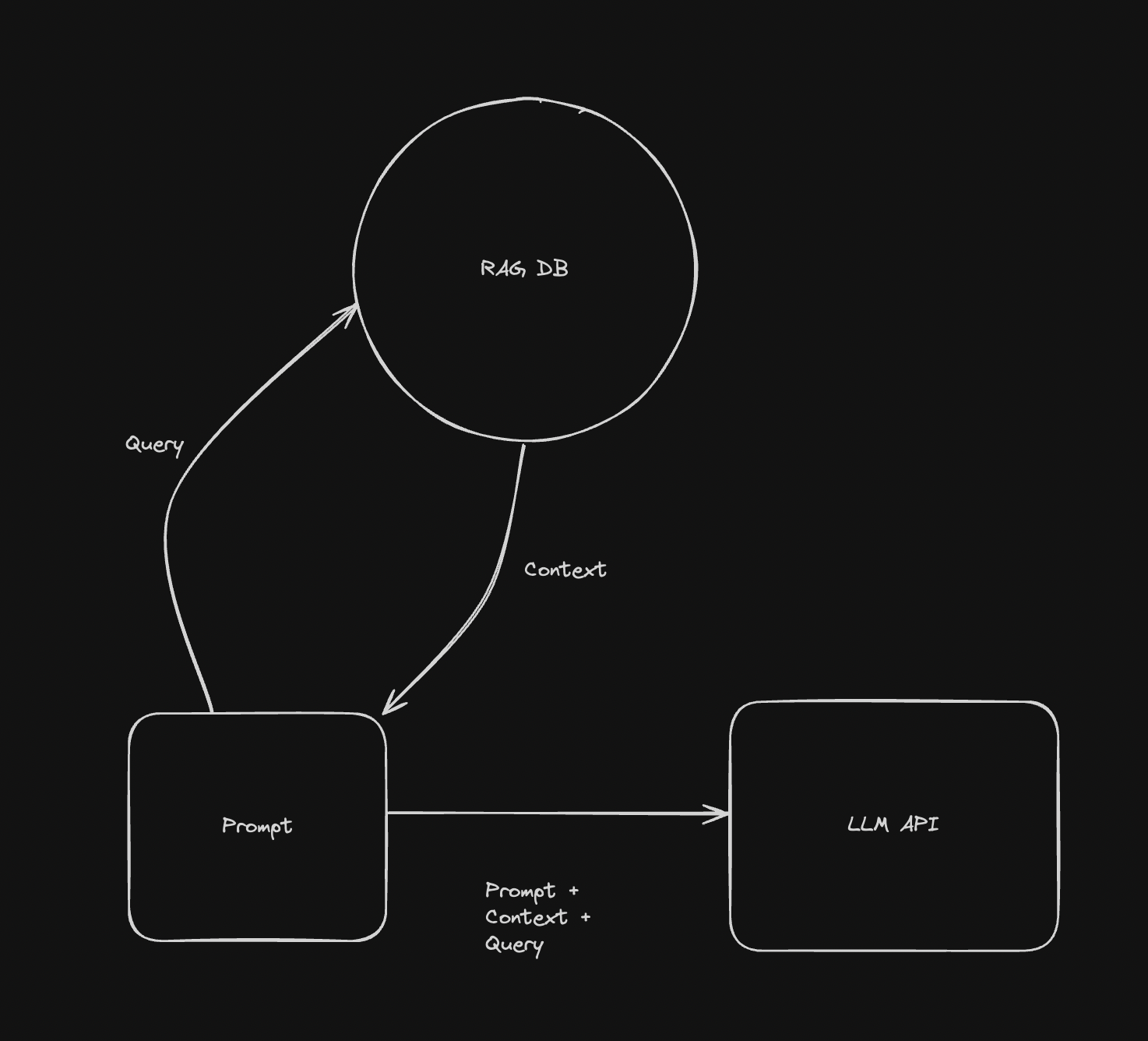
RAG is the process of determining what context to add. This is typically done by encoding the query into a vector space and then finding the closest vectors in the database to the query. Each vector represents hundreds or thousands of tokens.
Binary Vector Space
Why binary vector space?
It turns out the accuracy is very similar to a full 32-bit vector. But we save a lot in terms of server costs, and it makes in-memory retrieval more feasible.
A database that was once 1TB is now ~32GB, which can easily fit in RAM on a much cheaper setup.
Assuming each row is a 1024-dim float32 vector, that's 4096 bytes per row. or ~244 million rows.
For some added context Wikipedia, which is arguably the largest publicly available data to RAG might only be around 15 million rows.
https://en.wikipedia.org/wiki/Wikipedia:Size_of_Wikipedia
- 6,818,523 articles
- average 668 words per article (4.55B billion words)
- According to OpenAI 750 words is roughly 1000 tokens. So let's say 6B tokens.
- if we use the mixedbread model we can represent 512 tokens in a vector, assuming overlap let’s say 400 tokens new tokens in each vector with 112 being used for overlap
6B / 400 = ~15,000,000 vectors
Chances are internal RAGs are going to be significantly smaller than this.
And so this opens up the question:
"At what point is the dataset too big that exact brute search over binary vectors is not entirely feasible?"
If our dataset is smaller than this, then we can just do the dumb thing in a very small amount of code and be completely fine.
We might not need a fancy vector DB or the newest HSNW library (HNSW is approximate search anyway, we're doing exact).
I'm doing this in Julia because:
- I like it. :-)
- It should be able to get comparable performance for this relative to C, C++ or Rust. So we're not missing out on potential gains.
julia> versioninfo() Julia Version 1.11.0-beta1 Commit 08e1fc0abb9 (2024-04-10 08:40 UTC) Build Info: Official https://julialang.org/ release Platform Info: OS: macOS (arm64-apple-darwin22.4.0) CPU: 8 × Apple M1 WORD_SIZE: 64 LLVM: libLLVM-16.0.6 (ORCJIT, apple-m1) Threads: 4 default, 0 interactive, 2 GC (on 4 virtual cores) Environment: JULIA_STACKTRACE_MINIMAL = true DYLD_LIBRARY_PATH = /Users/lunaticd/.wasmedge/lib JULIA_EDITOR = nvim
Ok, let's begin!
Implementation
Each vector is going to be n bits, where n in the size of the embedding. This will vary depending on the embedder used, there are several proprietary and open source variations. I'll be assuming we're using the mixedbread model: mixedbread-ai/mxbai-embed-large-v1
This model returns a 1024 element float32 vector. Through binarization, this is converted into a 1024 bit vector, which is then represented as a 128 element int8 vector or 128 bytes. Additionally, this can be further reduced to 64 bytes, which is our final representation.
A 512 bit vector represented as 64 int8 or uint8 elements.
julia> x = rand(Int8, 64) 64-element Vector{Int8}: 26 123 70 -2 ⋮
Keep in mind that although the representation is in bytes we're operating at the bit level.
Comparing two bit vectors will require using the Hamming distance. Luckily the definition is very straightforward, each time a bit in the vectors doesn't match add 1 to the distance. So two bit vectors of length 512 that are entirely different will have a hamming distance of 512, and if they are the same a distance of 0.
An easy to do this is to turn the integer representation into a bitstring and then compute the distance on that.
julia> bitstring(Int8(125)) "01111101" julia> bitstring(Int8(33)) "00100001" julia> function hamming_distance(s1::AbstractString, s2::AbstractString)::Int s = 0 for (c1, c2) in zip(s1, s2) if c1 != c2 s += 1 end end s end julia> hamming_distance(bitstring(Int8(125)), bitstring(Int8(33))) # should be 4 4
Julia has a lovely benchmarking package called Chairmarks. Let's see how fast this implementation is.
julia> using Chairmarks julia> @be hamming_distance(bitstring(Int8(125)), bitstring(Int8(33))) Benchmark: 6053 samples with 317 evaluations min 36.672 ns (4 allocs: 128 bytes) median 38.514 ns (4 allocs: 128 bytes) mean 46.525 ns (4 allocs: 128 bytes, 0.13% gc time) max 8.737 μs (4 allocs: 128 bytes, 98.30% gc time)
This is honestly pretty good. For comparison let's do a simple addition:
julia> @be 125 + 33 Benchmark: 7274 samples with 8775 evaluations min 1.239 ns median 1.339 ns mean 1.453 ns max 6.990 ns
We're not going to get lower than this for an operation. The nanosecond is basically the atomic measurement unit for time when working with CPUs.
However, this does not mean each operation has to take ~1ns. There are various optimizations that hardware can do such that several operations are done each clock cycle. Each core of a CPU has a number of arithmetic units which are used to process elementary operations (addition, subtraction, xor, or, and, etc), the arithmetic units are fed by what is known as pipelining. The point is there is more than 1 arithmetic unit, so we can conceivably do several additons or bit operations in the same clock cycle as long as they do not depend on each other. Let's rewrite hamming_distance using only elementary operations so that we might take advantage of this.
Let's consider comparing two bits:
- 0, 0 -> 0
- 1, 0 -> 1
- 0, 1 -> 1
- 1, 1 -> 0
This is the XOR operation. We want to XOR all the bits and keep track of which ones are 1, and return the sum.
In order to do this over all the bits we can shift the integer by the number of bits, for an 8-bit number we would perform the shift 7 times.
Here's what this looks like:
@inline function hamming_distance(x1::T, x2::T)::Int where {T<:Union{Int8,UInt8}} r = x1 ⊻ x2 # xor # how many xored bits are 1 c = 0 for i in 0:7 c += (r >> i) & 1 end return Int(c) end # benchmark again julia> @be hamming_distance(Int8(33), Int8(125)) Benchmark: 4797 samples with 8966 evaluations min 2.175 ns median 2.189 ns mean 2.205 ns max 5.279 ns
This is huge improvement, almost as fast as doing an addition operation!
There's a builtin function in Julia count_ones lowers to a machine instruction popcnt that counts all the ones so we can just use that instead doing the shifts!
@inline function hamming_distance(x1::T, x2::T)::Int where {T<:Union{Int8,UInt8}} return Int(count_ones(x1 ⊻ x2)) end
Now it's the same as doing an addition operation!
julia> @be hamming_distance(Int8(33), Int8(125)) Benchmark: 5800 samples with 13341 evaluations min 1.243 ns median 1.249 ns mean 1.251 ns max 3.760 ns
Now we need to do this for an vector:
@inline function hamming_distance1(x1::AbstractArray{T}, x2::AbstractArray{T})::Int where {T<:Union{Int8,UInt8}} s = 0 for i in 1:length(x1) s += hamming_distance(x1[i], x2[i]) end s end
We expect this to take around 128ns (~2 * 64).
julia> @be hamming_distance1(q1, q2) Benchmark: 4469 samples with 256 evaluations min 69.500 ns median 75.035 ns mean 80.240 ns max 189.941 ns
There are a few more things we can do do further optimize this loop, the compiler sometimes does these automatically but we can manually annotate it to be certain.
@inline function hamming_distance(x1::AbstractArray{T}, x2::AbstractArray{T})::Int where {T<:Union{Int8,UInt8}} s = 0 @inbounds @simd for i in eachindex(x1, x2) s += hamming_distance(x1[i], x2[i]) end s end
@inboundsremoves any boundary checking.@simdtells the compiler to use SIMD instructions if possible.
julia> @be hamming_distance(q1, q2) Benchmark: 4441 samples with 323 evaluations min 52.759 ns median 56.245 ns mean 61.721 ns max 163.827 ns
That's a decent improvement. This benchmark is < 20ns on a fresh REPL session. I think it depends current background usage and how well SIMD can be utilized at that time.
julia> q1 = rand(Int8, 64); julia> q2 = rand(Int8, 64); julia> hamming_distance(q1, q2); julia> @be hamming_distance1(q1, q2) Benchmark: 4381 samples with 1113 evaluations min 17.932 ns median 18.381 ns mean 19.253 ns max 54.956 ns
It's good to know in a perfect environment, such as an isolated machine, you could make really good use of the hardware.
Let's say each comparison takes 50ns, then we can search over 20M rows in a second, or 80M rows if we used 4 cores.
1M rows should take 12ms over 4 cores. And Wikipedia at 15M rows 180ms.
In practice it turns out it's faster than this:
mutable struct MaxHeap const data::Vector{Pair{Int,Int}} current_idx::Int # add pairs until current_idx > length(data) const k::Int function MaxHeap(k::Int) new(fill((typemax(Int) => -1), k), 1, k) end end function insert!(heap::MaxHeap, value::Pair{Int,Int}) if heap.current_idx <= heap.k heap.data[heap.current_idx] = value heap.current_idx += 1 if heap.current_idx > heap.k makeheap!(heap) end elseif value.first < heap.data[1].first heap.data[1] = value heapify!(heap, 1)
The heap structure can be ignored, it's just a max heap with a maximum size. Each section of the database being searched has it's own heap and then sort and pick the top k results at the end.
Benchmarks
1M rows benchmark:
julia> X1 = [rand(Int8, 64) for _ in 1:(10^6)]; julia> k_closest(X1, q1, 1) 1-element Vector{Pair{Int64, Int64}}: 202 => 76839 julia> @be k_closest(X1, q1, 1) Benchmark: 17 samples with 1 evaluation min 5.571 ms (3 allocs: 112 bytes) median 5.618 ms (3 allocs: 112 bytes) mean 5.853 ms (3 allocs: 112 bytes) max 6.996 ms (3 allocs: 112 bytes) julia> k_closest_parallel(X1, q1, 1) 1-element Vector{Pair{Int64, Int64}}: 202 => 76839 julia> @be k_closest_parallel(X1, q1, 1) Benchmark: 32 samples with 1 evaluation min 3.022 ms (54 allocs: 3.672 KiB)
Each vector comparison is ~6ns rather than ~50ns.
But wait, There's more! We can do even better using StaticArrays:
julia> using StaticArrays julia> q1 = SVector{64, Int8}(rand(Int8, 64)); julia> X1 = [SVector{64, Int8}(rand(Int8, 64)) for _ in 1:(10^6)]; julia> @be k_closest(X1, q1, 1) Benchmark: 22 samples with 1 evaluation min 4.049 ms (3 allocs: 112 bytes) median 4.245 ms (3 allocs: 112 bytes) mean 4.453 ms (3 allocs: 112 bytes) max 6.010 ms (3 allocs: 112 bytes) julia> @be k_closest_parallel(X1, q1, 1) Benchmark: 86 samples with 1 evaluation min 1.120 ms (54 allocs: 3.672 KiB) median 1.133 ms (54 allocs: 3.672 KiB) mean 1.144 ms (54 allocs: 3.672 KiB) max 1.311 ms (54 allocs: 3.672 KiB)
Now each vector comparison is taking ~4ns! Also notice that the parallel implementation looks to be better utilizing the cores available, improvement the runtime by 4x, since we have 4 cores, instead of just 2x.
However, we don't want just closest vector, but the "k" closest ones, so let's set "k" to something more realistic:
julia> @be k_closest(X1, q1, 20) Benchmark: 22 samples with 1 evaluation min 4.033 ms (5 allocs: 832 bytes) median 4.267 ms (5 allocs: 832 bytes) mean 4.511 ms (5 allocs: 832 bytes) max 5.910 ms (5 allocs: 832 bytes) julia> @be k_closest_parallel(X1, q1, 20) Benchmark: 85 samples with 1 evaluation min 1.126 ms (56 allocs: 7.828 KiB) median 1.137 ms (56 allocs: 7.828 KiB) mean 1.142 ms (56 allocs: 7.828 KiB) max 1.194 ms (56 allocs: 7.828 KiB) julia> @be k_closest(X1, q1, 100) Benchmark: 23 samples with 1 evaluation min 4.108 ms (5 allocs: 3.281 KiB) median 4.270 ms (5 allocs: 3.281 KiB) mean 4.344 ms (5 allocs: 3.281 KiB) max 5.472 ms (5 allocs: 3.281 KiB)
Similar timings since we're using a heap to order the entries.
Just for fun let's search over 15M rows (Wikipedia).
julia> X1 = [SVector{64, Int8}(rand(Int8, 64)) for _ in 1:(15 * 10^6)]; julia> @be k_closest_parallel(X1, q1, 10) Benchmark: 6 samples with 1 evaluation min 16.534 ms (56 allocs: 5.625 KiB) median 16.637 ms (56 allocs: 5.625 KiB) mean 16.628 ms (56 allocs: 5.625 KiB) max 16.762 ms (56 allocs: 5.625 KiB) julia> @be k_closest_parallel(X1, q1, 50) Benchmark: 6 samples with 1 evaluation min 16.506 ms (58 allocs: 14.062 KiB) median 16.672 ms (58 allocs: 14.062 KiB) mean 16.669 ms (58 allocs: 14.062 KiB) max 16.777 ms (58 allocs: 14.062 KiB)
And over 100,000 rows:
julia> X1 = [SVector{64, Int8}(rand(Int8, 64)) for _ in 1:(10^5)]; julia> @be k_closest_parallel(X1, q1, 30) Benchmark: 679 samples with 1 evaluation min 120.250 μs (56 allocs: 10.000 KiB) median 131.792 μs (56 allocs: 10.000 KiB) mean 137.709 μs (56 allocs: 10.000 KiB) max 463.625 μs (56 allocs: 10.000 KiB)
Under 1ms!
usearch
usearch appears to be state of the art for in-memory vector similarity searches.
In [8]: from usearch.index import search, MetricKind ...: import numpy as np In [12]: X = np.random.randint(-128, 128, size=(10**6, 64), dtype=np.int8) In [13]: q = np.random.randint(-128, 128, 64, dtype=np.int8) In [14]: %timeit search(X, q, 1, MetricKind.Hamming, exact=True) 62.4 ms ± 494 µs per loop (mean ± std. dev. of 7 runs, 10 loops each) In [15]: %timeit search(X, q, 1, MetricKind.Hamming, exact=True, threads=4) 32.7 ms ± 1.7 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
The Julia implementation is ~16x faster single threaded and ~30x faster when using 4 cores.
Maybe there's a way to make usearch faster, and in all fairness exact search is likely not the priority to get as fast a possible.
That being said this is around 100 lines of Julia code and we're not doing anything fancy aside from arguably using StaticArrays.
Conclusion
With ~100 lines of Julia code we're able to achieve state of the art results in exact search similarity search for binary vector spaces.
I don't know about you but I think this is pretty damn awesome!
Extra
I realized I never answered the original question (my bad).
"At what point is the dataset too big that exact brute search over binary vectors is not entirely feasible?"
Well it depends, how many RPS do you need to handle? What is the upper limit on how long the query should take?
Right now were at ~1-1.3ms for 1M rows. 10M rows would be ~10-13ms.
julia> X1 = [SVector{64, Int8}(rand(Int8, 64)) for _ in 1:(20 * 10^6)]; julia> @be k_closest_parallel(X1, q1, 100) Benchmark: 5 samples with 1 evaluation min 22.198 ms (58 allocs: 23.906 KiB) median 22.232 ms (58 allocs: 23.906 KiB) mean 22.247 ms (58 allocs: 23.906 KiB) max 22.330 ms (58 allocs: 23.906 KiB)
Even at 20M rows this query is unlikely to be the bottleneck of the application. 20M rows would be 76GB of the original encoded data vectors: 1024 element 32-bit vector. That's a big dataset, do you have that dataset? Probably not.