Are LLMs useful because they overfit everything?

AI companies train their models on both public and private datasets, with the public datasets being an aggregation of the internet. Evaluating LLMs is notoriously difficult to trust because of this.

Did they just train on the evaluation dataset? Maybe. Probably. Especially publicly available ones. Companies use their own evaluation datasets for this very reason, and adept LLM users defer to competitions to see how the top models perform.

Let's say we were using LeetCode to evaluate whether the model is good at coding. Providing only the initial code as the prompt:

class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:

We don't mention any additional details about the problem or even say to complete the code, just paste and see what happens.

This is the output:

START OF OUTPUT

To solve the problem of finding the sum of the minimum values of all subarrays of a given array arr, we can use a stack-based approach to efficiently compute the contribution of each element as the minimum in various subarrays. Here's a step-by-step explanation and the corresponding Python code:

Explanation

1. Understanding the Contribution of Each Element:

   • For each element in the array, we need to determine how many subarrays it is the minimum for.
   • Specifically, for each element arr[i], we need to find:
     • left[i]: The number of contiguous subarrays ending at i where arr[i] is the minimum.
     • right[i]: The number of contiguous subarrays starting at i where arr[i] is the minimum.

2. Using Monotonic Stacks:

   • We use two monotonic stacks to compute left and right:
     • left[i] is computed by iterating from left to right and using a stack to keep track of the previous smaller elements.
     • right[i] is computed by iterating from right to left and using a stack to keep track of the next smaller elements.

3. Calculating the Result:

   • Once we have left and right arrays, the contribution of arr[i] to the total sum is arr[i] * left[i] * right[i].
   • Summing up these contributions for all elements gives the desired result.

4. Modulo Operation:

   • Since the result can be very large, we take the result modulo (10^9 + 7).

Python Code

Here's the complete implementation of the solution:

from typing import List

class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        MOD = 10**9 + 7
        n = len(arr)

        # Arrays to store the number of subarrays where arr[i] is the minimum
        left = [0] * n
        right = [0] * n

        # Monotonic stack for calculating left
        stack = []
        for i in range(n):
            # Count the number of subarrays ending at i where arr[i] is the minimum
            while stack and arr[stack[-1]] > arr[i]:
                stack.pop()
            left[i] = i + 1 if not stack else i - stack[-1]
            stack.append(i)

Explanation of the Code

• Initialization:

  • MOD is set to (10^9 + 7) to handle large numbers.
  • left and right arrays are initialized to store the number of subarrays where each element is the minimum.
  • stack is used to maintain indices of elements in a monotonic order.

• Calculating left:

  • We iterate through the array from left to right.
  • For each element, we pop elements from the stack until we find an element smaller than the current element.
  • left[i] is then set based on the position of the last element in the stack.

• Calculating right:

  • We iterate through the array from right to left.
  • For each element, we pop elements from the stack until we find an element smaller than or equal to the current element.
  • right[i] is then set based on the position of the last element in the stack.

• Calculating the Result:

  • We iterate through the array and sum up the contributions of each element, taking the modulo at each step to avoid overflow.

This approach ensures that we efficiently compute the desired sum in linear time, making it suitable for large input sizes.

END OF OUTPUT

The most striking of this to me is MOD = 10**9 + 7 because this is a direct mention to the Leetcode description:

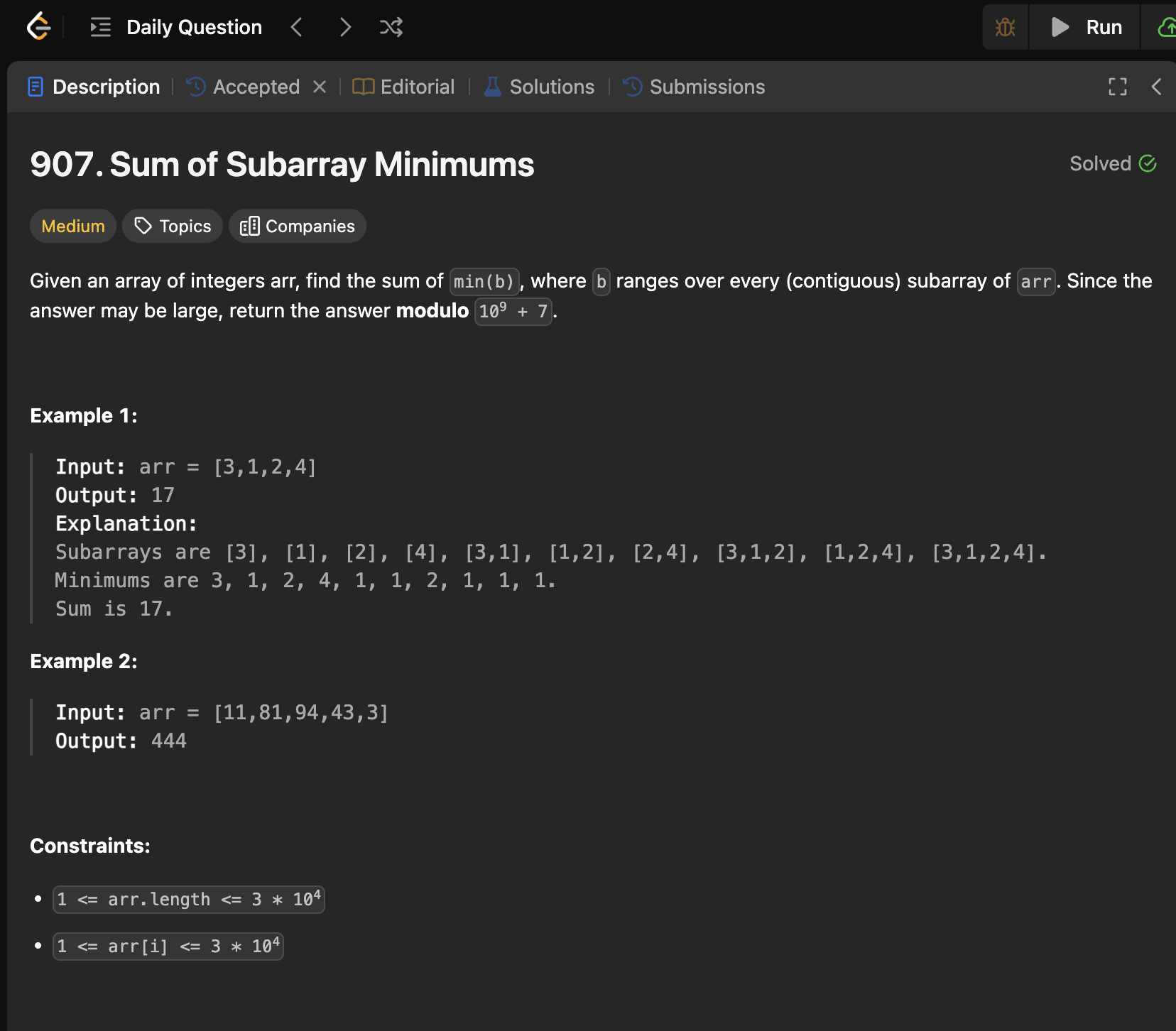
Clearly, there's data leakage; we never mentioned anything about a modulus or the presented value.

Is overfitting a concern with LLMs? Overfitting is a concern because the model won't generalize outside the training set, but if the training set is everything, why would that be an issue? Furthermore, perhaps grokking kicks in at some point, transitioning the model from a state of memorization to generalization.

If overfitting returns a compressed interactive compendium of all human knowledge then who cares.